The Competitiveness of Nations in a Global Knowledge-Based Economy
The Function of Measurement in
Modern Physical Science
|
II. Motives for Normal Measurement III. The Effects of Normal Measurement |
1. For the façade see, Eleven Twenty-Six: A Decade of Social Science Research, ed. Louis Wirth (Chicago, 1940), p. 169. The sentiment there inscribed recurs in Kelvin’s writings but I have found no formulation closer to the Chicago quotation than the following: “When you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind.” See Sir William Thomson, “Electrical Units of Measurement,” - grows out of the Berkeley colloquium. In de riving the present paper from it, I have prePopular Lectures and Addresses, 3 vols. (London, 1889-91), I, 73.
2. The central sections of this paper, which was added to the present program at a late date, are abstracted from my essay, “The Role of Measurement in the Development of Natural Science”, a multilithed revision of a talk first given to the Social Sciences Colloquium of the University of California, Berkeley. That version will be published in a volume of papers on “Quantification in the Social Sciences” that grows out of the Berkley colloquium. In deriving the present paper from it, I have prepared a new introduction and last section, and have somewhat condensed the material that intervenes.
161
central questions of this paper - how has measurement actually functioned in physical science, and what has been the source of its special efficacy - will be approached directly. For this purpose, and for it alone, history will truly be “philosophy teaching by example.”
Before permitting history to function even as a source of examples, we must, however, grasp the full significance of allowing it any function at all. To that end my paper opens with a critical discussion of what I take to be the most prevalent image of scientific measurement, an image that gains much of its plausibility and force from the manner in which computation and measurement enter into a profoundly unhistorical source, the science text. That discussion, confined to Section I below, will suggest that there is a textbook image or myth of science and that it may be systematically misleading. Measurement’s actual function - either in the search for new theories or in the confirmation of those already at hand - must be sought in the journal literature, which displays not finished and accepted theories, but theories in the process of development. After that point in the discussion, history will necessarily become our guide, and Sections II and III will attempt to present a more valid image of measurement’s most usual functions drawn from that source. Section IV employs the resulting description to ask why measurement should have proved so extraordinarily effective in physical research. Only after that, in the concluding section, shall I attempt a synoptic view of the route by which measurement has come increasingly to dominate physical science during the past three hundred years.
[One more caveat proves necessary before beginning. A few participants in this conference seem occasionally to mean by measurement any unambiguous scientific experiment or observation. Thus, Professor Boring supposes that Descartes was measuring when he demonstrated the inverted retinal image at the back of the eye-ball; presumably he would say the same about Franklin’s demonstration of the opposite polarity of the two coatings on a Leyden jar. Now I have no doubt that experiments like these are among the most significant and fundamental that the physical sciences have known, but I see no virtue in describing their results as measurements. In any case, that terminology would obscure what are perhaps the most important points to be made in this paper. I shall therefore suppose that a measurement (or a fully quantified theory) always produces actual numbers. Experiments like Descartes’ or Franklin’s, above, will be classified as qualitative or as non-numerical, without, I hope, at all implying that they are therefore less important. Only with that distinction between qualitative and quantitative available can I hope to show that large amounts of qualitative work have usually been prerequisite to fruitful quantification in the physical sciences. And only if that point can be made shall we be in a position even to ask about the effects of introducing quantitative methods into sciences that had previously proceeded without major assistance from them.]
To a very much greater extent than we ordinarily realize, our image of physical science and of measurement is conditioned by science texts. In part that
162
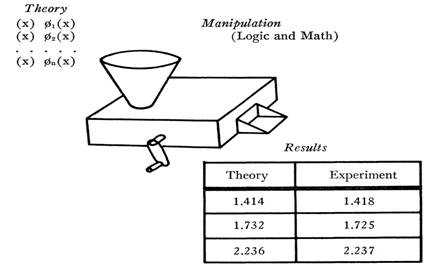
I shall shortly indicate why the textbook mode of presentation must inevitably be misleading, but let us first examine that presentation itself. Since most participants in this conference have already been exposed to at least one textbook of physical science, I restrict attention to the schematic tripartite summary in the following figure. It displays, in the upper left, a series of
3. This phenomenon is examined in more detail in my monograph, The Structure of Scientific Revolutions, to appear when completed as Vol. II, No. 2, in the International Encyclopedia of Unified Science. Many other aspects of the textbook image of science, its sources and its strengths, are also examined in that place.
4. Obviously not all the statements required to constitute most theories are of this particular logical form, but the complexities have no relevance to the points made here. R. B. Braithwaite, Scientific Explanation (Cambridge, England, 1953) includes a useful, though very general, description of the logical structure of scientific theories.
hopper at the top of the machine together with certain “initial conditions” specifying the situation to which the theory is being applied. The crank is then turned; logical and mathematical operations are internally performed; and numerical predictions for the application at hand emerge in the chute at the front of the machine. These predictions are entered in the left-hand column of the table that appears in the lower right of the figure. The right-hand column contains the numerical results of actual measurements, placed there so that they may be compared with the predictions derived from the theory. Most texts of physics, chemistry, astronomy, etc. contain many data of this sort, though they are not always presented in tabular form. Some of you will, for example, be more familiar with equivalent graphical presentations.
The table at the lower right is of particular concern, for it is there that the results of measurement appear explicitly. What may we take to be the significance of such a table and of the numbers it contains? I suppose that there are two usual answers: the first, immediate and almost universal; the other, perhaps more important, but very rarely explicit.
Most obviously the results in the table seem to function as a test of theory. If corresponding numbers in the two columns agree, the theory is acceptable; if they do not, the theory must be modified or rejected. This is the function of measurement as confirmation, here seen emerging, as it does for most readers, from the textbook formulation of a finished scientific theory. For the time being I shall assume that some such function is also regularly exemplified in normal scientific practice and can be isolated in writings whose purpose is not exclusively pedagogic. At this point we need only notice that on the question of practice, textbooks provide no evidence whatsoever. No textbook ever included a table that either intended or managed to infirm the theory the text was written to describe. Readers of current science texts accept the theories there expounded on the authority of the author and the scientific community, not because of any tables that these texts contain. If the tables are read at all, as they often are, they are read for another reason.
It is by no means obvious that our ideas about this function of numbers are related to the textbook schema outlined in the diagram above, yet I see no other way to account for the special efficacy often attributed to the results of measurement. We are, I suspect, here confronted with a vestige of an admittedly outworn belief that laws and theories can be arrived at by some
5 Professor Frank Knight, for example, suggests that to social scientists the “practical meaning [of Kelvin’s statement] tends to be: ‘If you cannot measure, measure anyhow.’” Eleven Twenty-Six, 169.
164
process like “running the machine backwards.” Given the numerical data in the “Experiment” column of the table, logico-mathematical manipulation (aided, all would now insist, by “intuition”) can proceed to the statement of the laws that underlie the numbers. If any process even remotely like this is involved in discovery - if, that is, laws and theories are forged directly from data by the mind - then the superiority of numerical to qualitative data is immediately apparent. The results of measurement are neutral and precise; they cannot mislead. Even more important, numbers are subject to mathematical manipulation; more than any other form of data, they can be assimilated to the semimechanical textbook schema.
I have already implied my skepticism about these two prevalent descriptions of the function of measurement. In Sections II and III each of these functions will be further compared with ordinary scientific practice. But it will help first critically to pursue our examination of textbook tables. By doing so I would hope to suggest that our stereotypes about measurement do not even quite fit the textbook schema from which they seem to derive. Though the numerical tables in a textbook do not there function either for exploration or confirmation, they are there for a reason. That reason we may perhaps discover by asking what the author of a text can mean when he says that the numbers in the “Theory” and “Experiment” column of a table “agree.”
It follows that what scientists seek in numerical tables is not usually “agree-
6. The first three Laws of Thermodynamics are well known outside the trade. The “Fourth Law” states that no piece of experimental apparatus works the first time it is set up. We shall examine evidence for the Fifth Law below.
7. T. S. Kuhn, The Copernican Revolution (Cambridge, Mass., 1957), PP. 72-76, 135-143.
8. William Ramsay, The Gases of the Atmosphere: the History of Their Discovery (London, 1896), Chapters 4 and 5.
9. To pursue this point would carry us far beyond the subject of this paper, but it should be pursued because, if I am right, it relates to the important contemporary controversy over the distinction between analytic and synthetic truth. To the extent that a scientific theory must be accompanied by a statement of the evidence for it in order to have empirical meaning, the full theory (which includes the evidence) must be analytically true. For a statement of the philosophical problem of analyticity see W. V. Quine, “Two Dogmas of Empiricism” and other essays in From a Logi-[cal Point of View (Cambridge, Mass., 1953). For a stimulating, but loose, discussion of the occasionally analytic status of scientific laws, see N. R. Hanson, Patterns of Discovery (Cambridge, England, 1958), pp. 93-118. A new discussion of the philosophical problem, including copious references to the controversial literature, is Alan Pasch, Experience and the Analytic: A Reconsideration of Empiricisin (Chicago, 1958).]
HHC: [bracketed] displayed on page 167 of original.
166
II. MOTIVES FOR NORMAL MEASUREMENT
10. The monograph cited in note 3 will argue that the misdirection supplied by science texts is both systematic and functional. It is by no means clear that a more accurate image of the scientific processes would enhance the research efficiency of physical scientists.
11. It is, of course, somewhat anachronistic to apply the terms “journal literature” and “textbooks” in the whole of the period I have been asked to discuss. But I am concerned to emphasize a pattern of professional communication whose origins at least can be found in the seventeenth century and which has increased in rigor ever since. There was a time (different in different sciences) when the pattern of communication in a science was much the same as that still visible in the humanities and many of the social sciences, but in all the physical sciences this pattern is at least a century gone, and in many of them it disappeared even earlier than that. Now all publication of research results occurs in journals read only by the profession. Books are exclusively textbooks, compendia, popularizations, or philosophical reflections, and writing them is a somewhat suspect, because nonprofessional activity. Needless to say this sharp and rigid separation between articles and books, research and nonresearch writings, greatly increases the strength of what I have called the textbook image
Probably the rarest and most profound sort of genius in physical science is that displayed by men who, like Newton, Lavoisier, or Einstein, enunciate a whole new theory that brings potential order to a vast number of natural phenomena. Yet radical reformulations of this sort are extremely rare, largely because the state of science very seldom provides occasion for them. Moreover, they are not the only truly essential and creative events in the development of scientific knowledge. The new order provided by a revolutionary new theory in the natural sciences is always overwhelmingly a potential order. Much work and skill, together with occasional genius, are required to make it actual. And actual it must be made, for only through the process of actualization can occasions for new theoretical reformulations be discovered. The bulk of scientific practice is thus a complex and consuming mopping-up operation that consolidates the ground made available by the most recent theoretical breakthrough and that provides essential preparation for the breakthrough to follow. In such mopping-up operations, measurement has its overwhelmingly most common scientific function.
Undoubtedly the general theory of relativity is an extreme case, but the situation it illustrates is typical. Consider, for a somewhat more extended example, the problem that engaged much of the best eighteenth-century scien-
12. Here and elsewhere in this paper I ignore the very large amount of measurement done simply to gather factual information. I think of such measurements as specific gravities, wave lengths, spring constants, boiling points, etc., undertaken in order to determine parameters that must be inserted into scientific theories but whose numerical outcome those theories do not (or did not in the relevant period) predict. This sort of measurement is not without interest, but I think it widely understood. In any case, considering it would too greatly extend the limits of this paper.
13. These are: the deflection of light in the sun’s gravitational field, the precession of the perihelion of Mercury, and the red shift of light from distant stars. Only the first two are actually quantitative predictions in the present state of the theory.
14. The difficulties in producing concrete applications of the general theory of relativity need not prevent scientists from attempting to exploit the scientific viewpoint embodied in that theory. But, perhaps unfortunately, it seems to be doing so. Unlike the special theory, general relativity is today very little studied by students of physics. Within fifty years we may conceivably have totally lost sight of his aspect of Einstein’s contribution.
168
15. The most relevant and widely employed experiments were performed with pendula. Determination of the recoil when two pendulum bobs collided seems to have been the main conceptual and experimental tool used in the seventeenth century to determine what dynamical “action” and “reaction” were. See A. Wolf, A History of Science, Technology, and Philosophy in the 16th & 17th Centuries, new ed. prepared by D. McKie (London, 1950), p. 155, 231-235; and R. Dugas, La mécanique zu xviie siècle (Neuchatel, 1954), pp. 283-298; and Sir Isaac Newton’s Mathematical Principles of Natural Philosophy and his System of the World, ed. F. Cajori (Berkeley, 1934), pp. 21-28. Wolf (p. 155) describes the Third Law as “the only physical law of the three.”
16. See the excellent description of this apparatus and the discussion of Atwood’s reasons for building it in Hanson, Patterns of Discovery, pp. 100-102 and notes to these pages.
17. A. Wolf, A History of Science, Technology, and Philosophy in the Eighteenth Century, 2nd ed. revised by D. McKie (London, 1952), pp. 111-113. There are some precursors of Cavendish’s measurements of 1798, but it is only after Cavendish that measurement begins to yield consistent results.
18. Modern laboratory apparatus designed to help students study Galileo’s law of free fall provides a classic, though perhaps quite necessary, example of the way pedagogy misdirects the historical imagination about the relation between creative science and measurement. None of the apparatus now used could possibly have been built in the seventeenth century. One of the best and most widely disseminated pieces of equipment, for example, allows a heavy bob to fall between a pair of parallel vertical rails. These rails are electrically charged every 1/100th of a second, and the spark that then passes through the bob from rail to rail records the bob’s position on a chemically treated tape. Other pieces of apparatus involve electric timers, etc. For the historical difficulties of making measurements relevant to this law, see below.
19. All the applications of Newton’s Laws involve approximations of some sort, but in the following examples the approximations [have a quantitative importance that they do not possess in those that precede.]
HHC – [bracketed] displayed on page 170 of original
As far as it goes, the situation illustrated by quantitative application of Newton’s Laws is, I think perfectly typical. Similar examples could be produced from the history of the corpuscular, the wave, or the quantum mechanical theory of light, from the history of electromagnetic theory, quantitative chemical analysis, or any other of the numerous natural scientific theories with quantitative implications. In each of these cases, it proved immensely difficult to find many problems that permitted quantitative comparison of theory and observation. Even when such problems were found, the highest scientific talents were often required to invent apparatus, reduce perturbing effects, and
20. Wolf, Eighteenth Century, pp. 75-81, provides a good preliminary description of this work.
170
estimate the allowance to be made for those that remained. This is the sort of work that most physical scientists do most of the time insofar as their work is quantitative. Its objective is, on the one hand, to improve the measure of “reasonable agreement” characteristic of the theory in a given application and, on the other, to open up new areas of application and establish new measures of “reasonable agreement” applicable to them. For anyone who finds mathematical or manipulative puzzles challenging, this can be fascinating and intensely rewarding work. And there is always the remote possibility that it will pay an additional dividend: something may go wrong.
Yet unless something does go wrong - a situation to be explored in Section IV - these finer and finer investigations of the quantitative match between theory and observation cannot be described as attempts at discovery or at confirmation. The man who is successful proves his talents, but he does so by getting a result that the entire scientific community had anticipated someone would someday achieve. His success lies only in the explicit demonstration of a previously implicit agreement between theory and the world. No novelty in nature has been revealed. Nor can the scientist who is successful in this sort of work quite be said to have “confirmed” the theory that guided his research. For if success in his venture “confirms” the theory, then failure ought certainly “infirm” it, and nothing of the sort is true in this case. Failure to solve one of these puzzles counts only against the scientist; he has put in a great deal of time on a project whose outcome is not worth publication; the conclusion to be drawn, if any, is only that his talents were not adequate to it. If measurement ever leads to discovery or to confirmation, it does not do so in the most usual of all its applications.
III. THE EFFECTS OF NORMAL MEASUREMENT
There is a second significant aspect of the normal problem of measurement in natural science. So far we have considered why scientists usually measure; now we must consider the results that they get when they do so. Immediately another stereotype enforced by textbooks is called in question. In textbooks the numbers that result from measurement usually appear as the archetypes of the “irreducible and stubborn facts” to which the scientist must, by struggle, make his theories conform. But in scientific practice, as seen through the journal literature, the scientist often seems rather to be struggling with facts, trying to force them into conformity with a theory he does not doubt. Quantitative facts cease to seem simply “the given.” They must be fought for and with, and in this fight the theory with which they are to be compared proves the most potent weapon. Often scientists cannot get numbers that compare well with theory until they know what numbers they should be making nature yield.
Part of this problem is simply the difficulty in finding techniques and instruments that permit the comparison of theory with quantitative measurements. We have already seen that it took almost a century to invent a machine that could give a straightforward quantitative demonstration of Newton’s Second Law. But the machine that Charles Atwood described in 1784 was not the first instrument to yield quantitative information relevant to that Law.
The preceding example illustrates the difficulties and displays the role of theory in reducing scatter in the results of measurement. There is, however, more to the problem. When measurement is insecure, one of the tests for reliability of existing instruments and manipulative techniques must inevitably be their ability to give results that compare favorably with existing theory. In some parts of natural science, the adequacy of experimental technique can be judged only in this way. When that occurs, one may not even speak of “insecure” instrumentation or technique, implying that these could be improved without recourse to an external theoretical standard.
22. For a modern English version of the original see Galileo Galilei, Dialogues Concerning Two New Sciences, trans. Henry Crew and A. De Salvio (Evanston and Chicago, 1946), pp. 171-172.
23. This whole story and more is brilliantly set forth in A. Koyré, “An Experiment in Measurement,” Proc. Amer. Phil. Soc., 1953, 97: 222-237.
24. Hanson, Patterns of Discovery, p. 101
172
Needless to say, Dalton’s search of the literature yielded some data that, in his view, sufficiently supported the Law. But - and this is the point of the illustration - much of the then extant data did not support Dalton’s Law at all. For example, the measurements of the French chemist Proust on the two oxides of copper yielded, for a given weight of copper, a weight ratio for oxygen of 1.47:1. On Dalton’s theory the ratio ought to have been 2:1, and Proust is just the chemist who might have been expected to confirm the prediction. He was, in the first place, a fine experimentalist. Besides, he was then engaged in a major controversy involving the oxides of copper, a controversy in which he upheld a view very close to Dalton’s. But, at the beginning of the nineteenth century, chemists did not know how to perform quantitative analyses that displayed multiple proportions. By 1850 they had learned, but only by letting Dalton’s theory lead them. Knowing what results they should expect from chemical analyses, chemists were able to devise techniques that got them. As a result chemistry texts can now state that quantitative analysis confirms Dalton’s atomism and forget that, historically, the relevant analytic techniques are based upon the very theory they are said to confirm. Before Dalton’s theory was announced, measurement did not give the same results. There are self-fulfilling prophecies in the physical as well as in the social sciences.
That example seems to me quite typical of the way measurement responds to theory in many parts of the natural sciences. I am less sure that my next, and far stranger, example is equally typical, but colleagues in nuclear physics assure me that they repeatedly encounter similar irreversible shifts in the results of measurement.
25 This is not, of course, Dalton’s original notation. In fact, I am somewhat modernizing and simplifying this whole account. It can be reconstructed more fully from: A. N. Meldrum, “The Development of the Atomic Theory: (1) Berthollet’s Doctrine of Variable Proportions,” Manch. Mem., 1910, 54: 1-16; and “(6) The Reception accorded to the Theory advocated by Dalton,” ibid., 1911, 55: 1-10; L. K. Nash, The Atomic Molecular Theory, Harvard Case Histories in Experimental Science, Case 4 (Cambridge, Mass., 1950) ; and “The Origins of Dalton’s Chemical Atomic Theory,” Isis, 1956, 47: 110-116. See also the useful discussions of atomic weight scattered through J. R. Partington, A Short History of Chemistry, 2nd ed. (London, 1951).
But today no one can explain how this triumph can have occurred. Laplace’s interpretation of Delaroche and Berard’s figures made use of the caloric theory in a region where our own science is quite certain that that theory differs from directly relevant quantitative experiment by about 40 per cent. There is, however, also a 12 per cent discrepancy between the measurements of Delaroche and Berard and the results of equivalent experiments today. We are no longer able to get their quantitative result. Yet, in Laplace’s perfectly straightforward and essential computation from the theory, these two discrepancies, experimental and theoretical, cancelled to give close final agreement between the predicted and measured speed of sound. We may not, I feel sure, dismiss this as the result of mere sloppiness. Both the theoretician and the experimentalists involved were men of the very highest caliber. Rather we must here see evidence of the way in which theory and experiment may guide each other in the exploration of areas new to both.
These examples may enforce the point drawn initially from the examples in the last section. Exploring the agreement between theory and experiment into new areas or to new limits of precision is a difficult, unremitting, and, for many, exciting job. Though its object is neither discovery nor confirmation, its appeal is quite sufficient to consume almost the entire time and attention of those physical scientists who do quantitative work. It demands the very best of their imagination, intuition, and vigilance. In addition - when combined with those of the last section - these examples may show something more. They may, that is, indicate why new laws of nature are so very seldom discovered simply by inspecting the results of measurements made without advance knowledge of those laws. Because most scientific laws have so few quantitative points of contact with nature, because investigations of those contact points usually demand such laborious instrumentation and approximation, and because nature itself needs to be forced to yield the appropriate results, the route from theory
26. T.S. Kuhn, “The Caloric Theory of Adiabatic Compression,” Isis, 1958, 49: 132-140.
174
or law to measurement can almost never be travelled backwards. Numbers gathered without some knowledge of the regularity to be expected almost never speak for themselves. Almost certainly they remain just numbers.
One more example may make clear at least some of the prerequisites for this exceptional sort of discovery. The experimental search for a law or laws describing the variation with distance of the forces between magnetized and between electrically charged bodies began in the seventeenth century and was actively pursued through the eighteenth. Yet only in the decades immediately preceding Coulomb’s classic investigations of 1785 did measurement yield even an approximately unequivocal answer to these questions. What made the difference between success and failure seems to have been the belated assimilation of a lesson learned from a part of Newtonian theory. Simple force laws, like the inverse square law for gravitational attraction, can generally be expected only between mathematical points or bodies that approximate to them. The more complex laws of attraction between gross bodies can be derived from the simpler law governing the attraction of points by summing all the forces between all the pairs of points in the two bodies. But these laws will seldom take a simple mathematical form unless the distance between the two bodies is large compared with the dimensions of the attracting bodies themselves. Under these circumstances the bodies will behave as points, and experiment may reveal the resulting simple regularity.
27. Marie Boas, Robert Boyle and Seventeenth-Century Chemistry (Cambridge, England, 1958), p. 44.
28. Much relevant material will be found in Duane Roller and Duane H. D. Roller, The Development of the Concept of Electric Charge: Electricity from the Greeks to Coulomb, Harvard Case Histories in Experimental Science, Case 8 (Cambridge, Mass., 1954), and in Wolf, Eighteenth Century, pp. 239-250, 268-271
This illustration shows once again how large an amount of theory is needed before the results of measurement can be expected to make sense. But, and this is perhaps the main point, when that much theory is available, the law is very likely to have been guessed without measurement. Coulomb’s result, in particular, seems to have surprised few scientists. Though his measurements were necessary to produce a firm consensus about electrical and magnetic attractions - they had to be done; science cannot survive on guesses - many practitioners had already concluded that the law of attraction and repulsion must be inverse square. Some had done so by simple analogy to Newton’s gravitational law; others by a more elaborate theoretical argument; still others from equivocal data. Coulomb’s Law was very much “in the air” before its discoverer turned to the problem. If it had not been, Coulomb might not have been able to make nature yield it.
[Repeated discussions of this Section indicate two respects in which my text may be misleading. Some readers take my argument to mean that the committed scientist can make nature yield any measurements that he pleases. A few of these readers, and some others as well, also think my paper asserts that for the development of science, experiment is of decidedly secondary importance when compared with theory. Undoubtedly the fault is mine, but I intend to be making neither of these points.
If what I have said is right, nature undoubtedly responds to the theoretical predispositions with which she is approached by the measuring scientist. But that is not to say either that nature will respond to any theory at all or that she will ever respond very much. Reexamine, for a historically typical example, the relationship between the caloric and dynamical theory of heat. In their abstract structures and in the conceptual entities they presuppose, these two theories are quite different and, in fact, incompatible. But, during the years
29. A fuller account would have to describe both the earlier and the later approaches as “Newtonian.” The conception that electric force results from effluvia is partly Cartesian but in the eighteenth century its locus-classicus was the aether theory developed in Newton’s Opticks. Coulomb’s approach and that of several of his contemporaries depends far more directly on the mathematical theory in Newton’s Principia. For the differences between these books, their influence in the eighteenth century, and their impact on the development of electrical theory, see I. B. Cohen, Franklin and Newton: An Inquiry into Speculative Newtonian Experimental Science and Franklin’s Work in Electricity as an Example Thereof. (Philadelphia, 1956).
176
when the two vied for the allegiance of the scientific community, the theoretical predictions that could be derived from them were very nearly the same (see the reference cited in note 26). If they had not been, the caloric theory would never have been a widely accepted tool of professional research nor would it have succeeded in disclosing the very problems that made transition to the dynamical theory possible. It follows that any measurement which, like that of Delaroche and Berard, “fit” one of these theories must have “very nearly fit” the other, and it is only within the experimental spread covered by the phrase “very nearly” that nature proved able to respond to the theoretical predisposition of the measurer.
That response could not have occurred with “any theory at all.” There are logically possible theories of, say, heat that no sane scientist could ever have made nature fit, and there are problems, mostly philosophical, that make it worth inventing and examining theories of that sort. But those are not our problems, because those merely “conceivable” theories are not among the options open to the practicing scientist. His concern is with theories that seem to fit what is known about nature, and all these theories, however different their structure, will necessarily seem to yield very similar predictive results. If they can be distinguished at all by measurements, those measurements will usually strain the limits of existing experimental techniques. Furthermore, within the limits imposed by those techniques, the numerical differences at issue will very often prove to be quite small. Only under these conditions and within these limits can one expect nature to respond to preconception. On the other hand, these conditions and limits are just the ones typical in the historical situation.
If this much about my approach is clear, the second possible misunderstanding can be dealt with more easily. By insisting that a quite highly developed body of theory is ordinarily prerequisite to fruitful measurement in the physical sciences, I may seem to have implied that in these sciences theory must always lead experiment and that the latter has at best a decidedly secondary role. But that implication depends upon identifying “experiment” with “measurement,” an identification I have already explicitly disavowed. It is only because significant quantitative comparison of theories with nature comes at such a late stage in the development of a science that theory has seemed to have so decisive a lead. If we had been discussing the qualitative experimentation that dominates the earlier developmental stages of a physical science and that continues to play a role later on, the balance would be quite different. Perhaps, even then, we would not wish to say that experiment is prior to theory (though experience surely is), but we would certainly find vastly more symmetry and continuity in the ongoing dialogue between the two. Only some of my conclusions about the role of measurement in physical science can be readily extrapolated to experimentation at large.]
To this point I have restricted attention to the role of measurement in the normal practice of natural science, the sort of practice in which all scientists are mostly, and most scientists are always, engaged. But natural science also
displays abnormal situations - times when research projects go consistently astray and when no usual techniques seem quite to restore them - and it is through these rare situations that measurement shows its greatest strengths. In particular, it is through abnormal states of scientific research that measurement comes occasionally to play a major role in discovery and in confirmation.
30. See note 3
31. A recent example of the factors determing pursuit of an anomaly has been investigated by Bernard Barber and Renée C. Fox,. “The Case of the Floppy-Eared Rabbits: An Instance of Serendipity Gained and Serendipity - Lost,” Amer. Soc. Rev., 1958, 64: 128-136.
178
This is, of course, an immensely condensed and schematic description. Unfortunately, it will have to remain so, for the anatomy of the crisis state in natural science is beyond the scope of this paper. I shall remark only that these crises vary greatly in scope: they may emerge and be resolved within the work of an individual; more often they will involve most of those engaged in a particular scientific specialty; occasionally they will engross most of the members of an entire scientific profession. But, however widespread their impact, there are only a few ways in which they may be resolved. Sometimes, as has often happened in chemistry and astronomy, more refined experimental techniques or a finer scrutiny of the theoretical approximations will eliminate the discrepancy entirely. On other occasions, though I think not often, a discrepancy that has repeatedly defied analysis is simply left as a known anomaly, encysted within the body of more successful applications of the theory. Newton’s theoretical value for the speed of sound and the observed precession of Mercury’s perihelion provide obvious examples of effects which, though since explained, remained in the scientific literature as known anomalies for half a century or more. But there are still other modes of resolution, and it is they which give crises in science their fundamental importance. Often crises are resolved by the discovery of a new natural phenomenon; occasionally their resolution demands a fundamental revision of existing theory.
32. From Pasteur’s inaugural address at Lille in 1854 as quoted in René Vallery-Radot, La Vie de Pasteur (Paris, 1903), P. 88.
33. Angus Armitage, A Century of Astronomy (London, 1950), pp. 111-115.
34. For chlorine see Ernst von Meyer, A History of Chemistry from the Earliest Times to the Present Day, trans. G. M’Gowan (Lonion, 1891), pp. 224-227. For carbon monoxide see J. R. Partington, A Short History of [Chemistry, 2nd ed.. (London, 19’R5), pp. 140-141; and J. R. Partington and D. McKie, “Historical Studies of the Phlogiston Theory: IV. Last Phases of the Theory,” Annals of Science, 1939, 4: 365.]
HHC – [bracketed] displayed on page 180 of original
The case both for crises and for measurement becomes vastly stronger as soon as we turn from the discovery of new natural phenomena to the invention of fundamental new theories. Though the sources of individual theoretical inspiration may be inscrutable (certainly they must remain so for this paper), the conditions under which inspiration occurs is not. I know of no fundamental theoretical innovation in natural science whose enunciation has not been preceded by clear recognition, often common to most of the profession, that something was the matter with the theory then in vogue. The state
35.See note 7.
36. For useful surveys of the experiments which led to the discovery of the electron see T. W. Chalmers, Historic Researches: Chapters in the History of Physical and Chemical Discovery (London, 1949), pp. 187-217, and J. J. Thomson, Recollections and Reflections (New York, 1937), pp. 325-371. For electron-spin see F. K. Richtmeyer, E. H. Kennard, and T. Lauritsen, Introduction to Modern Physics, 5th ed. (New York, 1955), p. 212.
37. Rogers D. Rusk, Introduction to Atomic and Nuclear Physics (New York, 1958), pp 328-330. I know of no other elementary account recent enough to include a description of the physical detection of the neutrino.
38. Because scientific attention is often concentrated upon problems that seem to display anomaly, the prevalence of discovery-through. anomaly may be one reason for the prevalence of simultaneous discovery in the sciences. For evidence that it is not the only one see T. S Kuhn, “Conservation of Energy as an Example of Simultaneous Discovery,” Critical Problems in the History of Science, ed. Marshal Clagett (Madison, 1959), pp. 321-356, but notice that much of what is there said about the emergence of “conversion processes” also describes the evolution of a crisis state.
180
I suggest, therefore, that though a crisis or an “abnormal situation” is only
39. Kuhn, Copernican Revolution, pp. 138-140, 270-271; A. R. Hall, The Scientific Revolution, 1500-1800 (London, 1954), PP. 13-17. Note particularly the role of agitation for calendar reform in intensifying the crisis.
40. Kuhn, Copernican Revolution, pp. 237-260, and items in bibliography on pp. 290-291.
41. For Newton see T. S. Kuhn, “Newton’s Optical Papers,” in Isaac Newton’s Papers & Letters on Natural Philosophy, ed. I. B. Cohen (Cambridge, Mass., 1958), pp. 27-45. For the wave theory see E. T. Whittaker, History of the Theories of Aether and Electricity, The Classical Theories, 2nd ed. (London, 1951), pp. 94-109, and Whewell, Inductive Sciences, II, 396-466. These references clearly delineate the crisis that characterized optics when Fresnel independently began to develop the wave theory after 1812. But they say too little about eighteenth-century developments to indicate a crisis prior to Young’s earlier defense of the wave theory in and after 1801. In fact, it is not altogether clear that there was one, or at least that there was a new one. Newton’s corpuscular theory of light had never been quite universally accepted, and Young’s early opposition to it was based entirely upon anomalies that had been generally recognized and often exploited before. We may need to conclude that most of the eighteenth century was characterized by a low-level crisis in optics, for the dominant theory was never immune to fundamental criticism and attack.
That would be sufficient to make the point that is of concern here, but I suspect a careful study of the eighteenth-century optical literature will permit a still stronger conclusion. A cursory look at that body of literature suggests that the anomalies of Newtonian optics were far more apparent and pressing in the two decades before Young’s work than they had been before. During the l780’s the availability of achromatic lenses and prisms led to numerous proposals for an astronomical determination of the relative motion of the sun and stars. (The references in Whittaker, op. cit., p. 109, lead directly to a far larger literature.) But these all depended upon light’s moving more quickly in glass than in air and thus gave new relevance to an old controversy. L’Abbé Haüy demonstrated experimentally (Mem. de l’Acad. [1788], pp. 34-60) that Huyghen’s wave-theoretical treatment of double refraction had yielded better results than Newton’s corpuscular treatment. The resulting problem leads to the prize offered by the French Academy in 1808 and thus to Malus’ discovery of polarization by reflection in the same year. Or again, the Philosophical Transactions for 1796, 1797, and 1798 contain a series of two articles by Brougham and a third by Prevost which show still other difficulties in Newton’s theory. According to Prevost, in particular, the sorts of forces which must be exerted on light at an interface in order to explain reflection and refraction are not compatible with the sorts of forces needed to explain inflection (Phil. Trans., 1798, 84: 325-328. Biographers of Young might pay more attention than they have to the two Brougham papers in the preceding volumes. These display an intellectual commitment that goes a long way to explain Brougham’s subsequent vitriolic attack upon Young in the pages of the Edinburgh Review.)
42. Richtmeyer et al., Modern Physics, pp. 89-94, 124-132, and 409-414. A more elementary account of the black-body problem and of the photoelectric effect is included in Gerald Holton, Introduction to Concepts and Theories jn Physical Science (Cambridge, Mass., 1953), pp. 528-545.
one of the routes to discovery in the natural sciences, it is prerequisite to fundamental inventions of theory. Furthermore, I suspect that in the creation of the particularly deep crisis that usually precedes theoretical innovation, measurement makes one of its two most significant contributions to scientific advance. Most of the anomalies isolated in the preceding paragraph were quantitative or had a significant quantitative component, and, though the subject again carries us beyond the bounds of this essay, there is excellent reason why this should have been the case.
No crisis is, however, so hard to suppress as one that derives from a quantitative anomaly that has resisted all the usual efforts at reconciliation. Once the relevant measurements have been stabilized and the theoretical approximations fully investigated, a quantitative discrepancy proves persistently obtrusive to a degree that few qualitative anomalies can match. By their very nature, qualitative anomalies usually suggest ad hoc modifications of theory that will disguise them, and once these modifications have been suggested there is little way of telling whether they are “good enough.” An established quantitative anomaly, in contrast, usually suggests nothing except trouble, but at its best it provides a razor-sharp instrument for judging the adequacy of proposed solutions. Kepler provides a brilliant case in point. After prolonged struggle to rid astronomy of pronounced quantitative anomalies in the motion of Mars, he invented a theory accurate to 8’ of arc, a measure of agreement that would have astounded and delighted any astronomer who did not have access to the brilliant observations of Tycho Brahe. But from long experience Kepler knew Brahe’s observations to be accurate to 4’ of arc. To us, he said, Divine goodness has given a most diligent observer in Tycho Brahe, and it is therefore right that we should with a grateful mind make use of this gift to find the true celestial motions. Kepler next attempted computations with non-
43. Evidence for this effect of prior experience with a theory is provided by the well-known, but inadequately investigated, youthfulness of famous innovators as well as by the way in which younger men tend to cluster to the newer theory. Planck’s statement about the latter phenomenon needs no citation. An earlier and particularly moving version of the same sentiment is provided by Darwin in the last chapter of The Origin of Species. (See the 6th ed. [New York, 1889], II, 295-296.)
182
These examples were introduced to illustrate how difficult it is to explain away established quantitative anomalies, and to show how much more effective these are than qualitative anomalies in establishing unevadable scientific crises. But the examples also show something more. They indicate that measurement can be an immensely powerful weapon in the battle between two
44. J. L. E. Dreyer, A History of Astronomy from Thales to Kepler, 2nd ed. (New York, 1953), pp. 385-393.
45. Kuhn, “Newton’s Optical Papers,” pp. 31-36.
46. This is a slight oversimplification, since the battle between Lavoisier’s new chemistry and its opponents really implicated more than combustion processes, and the full range of relevant evidence cannot be treated in terms of combustion alone. Useful elementary accounts of Lavoisier’s contributions can be found in: B. Conant, The Overthrow of the Phlogiston Theory, Harvard Case Histories in Experimental Science, Case 2 (Cambridge, Mass., 1950), and D. McKie, Antoine Lavoisier: Scientist, Economist, Social Reformer (New York, 1952). Maurice Daumas, Lavoisier, Théoricien et expérimenteur (Paris, 1955) is the best recent scholarly review. J. H. White, The Phlogiston Theory (London, 1932) and especially J. R. Partington and D. McKie, “Historical Studies of the Phlogiston Theory: IV. Last Phases of the Theory,” Annals of Science, 1939, 4: 113-149, give most detail about the conflict between the new theory and the old.
theories, and that, I think, is its second particularly significant function. Furthermore, it is for this function - aid in the choice between theories - and for it alone, that we must reserve the word “confirmation.” We must, that is, if “confirmation” is intended to denote a procedure anything like what scientists ever do. The measurements that display an anomaly and thus create crisis may tempt the scientist to leave science or to transfer his attention to some other part of the field. But, if he stays where he is, anomalous observations, quantitative or qualitative, cannot tempt him to abandon his theory until another one is suggested to replace it. Just as a carpenter, while he retains his craft, cannot discard his toolbox because it contains no hammer fit to drive a particular nail, so the practitioner of science cannot discard established theory because of a felt inadequacy. At least he cannot do so until shown some other way to do his job. In scientific practice the real confirmation questions always involve the comparison of two theories with each other and with the world, not the comparison of a single theory with the world. In these three-way comparisons, measurement has a particular advantage.
47. This point is central to the reference cited in note 3. In fact, it is largely the necessity of balancing gains and losses and the controversies that so often result from disagreements about an appropriate balance that make it appropriate to describe changes of theory as “revolutions.”
48. Cohen, Franklin and Newton, Chapter 4; Pierre Brunet, L’introduction des theories de Newton en France au xviie siècle (Paris, 1931).
49. On this traditional task of chemistry see E. Meyerson, Identity and Reality, trans. K. Lowenberg (London, 1930), Chapter X, particularly pp. 331-336. Much essential material is also scattered through Hélène Metzger, Les xviie a la fin du xviiie siècle, vol. I (Paris, 1923), and Newton, Stahl, Boerhaave, et la doctrine chimique (Paris, 1930). Notice particularly that the phlogistonists, who looked upon ores as elementary bodies from which the metals were compounded by addition of phlogiston, could explain why the metals were so much more like each other than were the ores from which they were compounded. All metals had a principle, phlogiston, in common. No such explanation was possible on Lavoisier’s theory.
184
eral relativity does explain gravitational attraction, and quantum mechanics does explain many of the qualitative characteristics of bodies. We now know what makes some bodies yellow and others transparent, etc. But in gaining this immensely important understanding, we have had to regress, in certain respects, to an older set of notions about the bounds of scientific inquiry. Problems and solutions that had to be abandoned in embracing classic theories of modern science are again very much with us.
The study of the confirmation procedures as they are practiced in the sciences is therefore often the study of what scientists will and will not give up in order to gain other particular advantages. That problem has scarcely even been stated before, and I can therefore scarcely guess what its fuller investigation would reveal. But impressionistic study strongly suggests one significant conclusion. I know of no case in the development of science which exhibits a loss of quantitative accuracy as a consequence of the transition from an earlier to a later theory. Nor can I imagine a debate between scientists in which, however hot the emotions, the search for greater numerical accuracy in a previously quantified field would be called “unscientific.” Probably for the same reasons that make them particularly effective in creating scientific crises, the comparison of numerical predictions, where they have been available, has proved particularly successful in bringing scientific controversies to a close. Whatever the price in redefinitions of science, its methods, and its goals, scientists have shown themselves consistently unwilling to compromise the numerical success of their theories. Presumably there are other such desiderata as well, but one suspects that, in case of conflict, measurement would be the consistent victor.
V. MEASUREMENT IN THE DEVELOPMENT OF PHYSICAL SCIENCE
To this point we have taken for granted that measurement did play a central role in physical science and have asked about the nature of that role and the reasons for its peculiar efficacy. Now we must ask, though too late to anticipate a comparably full response, about the way in which physical science came to make use of quantitative techniques at all. To make that large and factual question manageable, I select for discussion only those parts of an answer which relate particularly closely to what has already been said.
One recurrent implication of the preceding discussion is that much qualitative research, both empirical and theoretical, is normally prerequisite to fruitful quantification of a given research field. In the absence of such prior work, the methodological directive, “Go ye forth and measure,” may well prove only an invitation to waste time. If doubts about this point remain, they should be quickly resolved by a brief review of the role played by quantitative techniques in the emergence of the various physical sciences. Let me begin by asking what role such techniques had in the scientific revolution that centered in the seventeenth century.
Since any answer must now be schematic, I begin by dividing the fields of physical science studied during the seventeenth century into two groups. The
185
50. Boas, Robert Boyle, pp. 48-66.
51. For electricity see, Roller and Roller, Concept of Electric Charge, Harvard Case Histories in Experimental Science, Case 8 (Cambridge, Mass., 1954), and, Edgar Zilsel, “The Origins of William Gilbert’s Scientific Method,” J. Hist. Ideas, 1941, 2: 1-32. I agree with those who feel Zilsel exaggerates the importance of a single factor in the genesis of electrical science and, by implication, of Baconianism, but the craft influences he describes cannot conceivably be dismissed. There is no equally satisfactory discussion of the development of thermal science before the eighteenth century, but Wolf, 16th and 17th Centuries, pp. 82-92 and 275-281 will illustrate the transformation produced by Baconianism.
52.Wolf, Eighteenth Century, pp. 102-145, and Whewell, Inductive Sciences, pp. 213-371. Particularly in the latter, notice the difficulty in separating advances due to improved instrumentation from those due to improved theory. This difficulty is not due primarily to Whewell’s mode of presentation.
53. For pre-Galilean work see, Marshall Clagett, The Science of Mechanics in the Middle Ages (Madison, Wis., 1959), particularly Parts II & III. For Galileo’s use of this work see, Alexandre Koyré, Etudes Galiléennes, 3 vols. (Paris, 1939), particularly I & II.
54. A. C. Crombie, Augustine to Galileo (London, 1952), pp. 70-82, and Wolf, 16th & 17th Centuries, pp. 244-254.
55. Ibid., pp. 254-264.
56. For the seventeenth-century work (including Huyghen’s geometric construction) see the reference in the preceding note. The eighteenth-century investigations of these phenomena have scarcely been studied, but for what is known see, Joseph Priestley, History of… Discoveries relating to Vision, Light, and Colours (London, 1772), pp. 279-316, 498-520, 548-562. The earliest examples I know of more precise work on double refraction are R. J. Haüy, “Sur Ia double refraction du Spath d’Islande,” Mem. d l’Acad. (1788), pp. 34-61, and, W. H. Wollaston, “On the oblique Refraction of Iceland Crystal,” Phil. Trans., 1802, 92: 381-386.
187
discovered during the Scientific Revolution, most of the eighteenth century was needed for the additional exploration and instrumentation prerequisite to quantitative exploitation.
Since Professor Guerlac’s paper is devoted to chemistry and since I have already sketched some of the bars to quantification of electrical and magnetic phenomena, I take my single more extended illustration from the study of heat. Unfortunately, much of the research upon which such a sketch should be based remains to be done. What follows is necessarily more tentative than what has gone before.
Many of the early experiments involving thermometers read like investigations of that new instrument rather than like investigations with it. How
57. See LH.B. and A.G.H. Spiers, The Physical Treatises of Pascal (New York, 1937), p. 164. This whole volume displays the way in which seventeenth-century pneumatics took over concepts from hydrostatics.
58. For the quantification and early mathematization of electrical science, see: Roller and Roller, Concept of Electric Charge, pp. 66-80; Whittaker, Aether and Electricity, pp. 53-66; and W. C. Walker, “The Detection and Estimation of Electric Charge in the Eighteenth Century,” Annals of Science, 1936, 1: 66-100.
59. For heat see, Douglas McKie and N. H. de V. Heathcote, The Discovery of Specific and Latent Heats (London, 1935). In chemistry it may well be impossible to fix any date for the “first effective contacts between meas[urement and theory.” Volumetric or gravimetric measures were always an ingredient of chemical recipes and assays. By the seventeenth century, for example in the work of Boyle, weight-gain or loss was often a clue to the theoretical analysis of particular reactions. But until the middle of the eighteenth century, the significance of chemical measurement seems always to have been either descriptive (as in recipes) or qualitative (as in demonstrating a weight-gain without significant reference to its magnitude). Only in the work of Black, Lavoisier, and Richter does measurement begin to play a fully quantitative role in the development of chemical laws and theories. For an introduction to these men and their work see, J. B. Partington, A Short History of Chemistry, 2nd ed. (London, 1951), pp. 93-97, 122-128, and 161-163.]
HHC – [bracketed] displayed on page 189 of original.
This sort of pattern, reiterated both in the other Baconian sciences and in the extension of traditional sciences to new instruments and new phenomena, thus provides one additional illustration of this paper’s most persistent thesis. The road from scientific law to scientific measurement can rarely be traveled
60. Maurice Daumas, Les instruments scientifiques aux XVIIe et XVIIIe siècles (Paris, 1953), pp. 78-80, provides an excellent brief account of the slow stages in the deployment of the thermometer as a scientific instrument. Robert Boyle’s New Experiments and Observations Touching Cold illustrates the seventeenth century’s need to demonstrate that properly constructed thermometers must replace the senses in thermal measurements even though the two give divergent results. See Works of the Honourable Robert Boyle, ed. T. Birch, 5 vols. (London, 1744), II, 240-243.
61. For the elaboration of calorimetric concepts see, E. Mach, Die Principien der Warmelehre (Leipzig, 1919), pp. 153-181, and McKie and Heathcote, Specific and Latent Heats. The discussion of Krafft’s work in the latter (pp. 59-63) provides a particularly striking example of the problems in making measurement work.
62. Gaston Bachelard, Etude sur l’évolution d’un problème de physique (Paris, 1928), and Kuhn, “Caloric Theory of Adiabatic Compression”.
189
Pending that test, can we conclude anything at all? I venture the following paradox: The full and intimate quantification of any science is a consummation devoutly to be wished. Nevertheless, it is not a consummation that can effectively be sought by measuring. As in individual development, so in the scientific group, maturity comes most surely to those who know how to wait.
63. S. F. Mason, Main Currents of Scientific Thought (New York, 1956), pp. 352-363, provides an excellent brief sketch of these institutional changes. Much additional material is scattered through, J. T. Merz, History of European Thought in the Nineteenth Century, vol. I (London, 1923).
64. For an example of effective problem selection, note the esoteric quantitative discrepancies which isolated the three problems - photoelectric effect, black body radiation, and specific heats - that gave rise to quantum mechanics. For the new effectiveness of verification procedures, note the speed with which this radical new theory was adopted by the profession.
190
Reflecting on the other papers and on the discussion that continued throughout the conference, two additional points that had reference to my own paper seem worth recording. Undoubtedly there were others as well, but my memory has proved more than usually unreliable. Professor Price raised the first point, which gave rise to considerable discussion. The second followed from an aside by Professor Spengler, and I shall consider its consequences first.
Professor Spengler expressed great interest in my concept of “crises” in the development of a science or of a scientific specialty, but added that he had had difficulty discovering more than one such episode in the development of economics. This raised for me the perennial, but perhaps not very important question about whether or not the social sciences are really sciences at all. Though I shall not even attempt to answer it in that form, a few further remarks about the possible absence of crises in the development of a social science may illuminate some part of what is at issue.
Professor Price’s point was very different and far more historical. He suggested, and I think quite rightly, that my historical epilogue failed to call attention to a very important change in the attitude of physical scientists towards measurement that occurred during the Scientific Revolution. In com-
65. I have developed some other significant concomitants of this professional consensus in my paper, “The Essential Tension: Tradition and Innovation in Scientific Research.” That paper appears in, Calvin W. Taylor (ed.), The Third (1959) University of Utah Research Conference on the Identification of Creative Scientific Talent (University of Utah Press, 1959), pp. 162-177.
rnenting on Dr. Crombie’s paper, Price had pointed out that not until the late sixteenth century did astronomers begin to record continuous series of observations of planetary position. (Previously they had restricted themselves to occasional quantitative observations of special phenomena.) Only in that same late period, he continued, did astronomers begin to be critical of their quantitative data, recognizing, for example, that a recorded celestial position is a clue to an astronomical fact rather than the fact itself. When discussing my paper, Professor Price pointed to still other signs of a change in the attitude towards measurement during the Scientific Revolution. For one thing, he emphasized, many more numbers were recorded. More important, perhaps, people like Boyle, when announcing laws derived from measurement, began for the first time to record their quantitative data, whether or not they perfectly fit the law, rather than simply stating the law itself.
I am somewhat doubtful that this transition in attitude towards numbers proceeded quite so far in the seventeenth century as Professor Price seemed occasionally to imply. Hooke, for one example, did not report the numbers from which he derived his law of elasticity; no concept of “significant figures” seems to have emerged in the experimental physical sciences before the nineteenth century. But I cannot doubt that the change was in process and that it is very important. At least in another sort of paper, it deserves detailed examination which I very much hope it will get. Pending that examination, however, let me simply point out how very closely the development of the phenomena emphasized by Professor Price fits the pattern I have already sketched in describing the effects of seventeenth-century Baconianism.
Furthermore, whether or not its source lies in Baconianism, the effectiveness of the seventeenth-century’s new attitude towards numbers developed in very much the same way as the effectiveness of the other Baconian novelties discussed in my concluding section. In dynamics, as Professor Koyré has repeatedly shown, the new attitude had almost no effect before the later eighteenth century. The other two traditional sciences, astronomy and optics, were affected sooner by the change, but only in their most nearly traditional parts.
66. See particularly his Robert Grosseteste 1700 (Oxford, 1953). and the Origins of Experimental Science, 1100-1700 (Oxford, 1953).
192
And the Baconian sciences, heat, electricity, chemistry, etc., scarcely begin to profit from the new attitude until after 1750. Again it is in the work of Black, Lavoisier, Coulomb, and their contemporaries that the first truly significant effects of the change are seen. And the full transformation of physical science due to that change is scarcely visible before the work of Ampere, Fourier, Ohm, and Kelvin. Professor Price has, I think, isolated another very significant seventeenth-century novelty. But like so many of the other novel attitudes displayed by the “new philosophy,” the significant effects of this new attitude towards measurement were scarcely manifested in the seventeenth century at all.
193